TRASLACIÓN
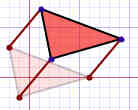Movimiento de una figura, sin rotarla ni voltearla. "Deslizar".La figura sigue viéndose exactamente igual, solo que en un lugar diferente.
Se realiza una traslación de un punto sencillo de coordenadas, mediante la inclusión de compensaciones en sus propias coordenadas, para generar una nueva posición de coordenadas. En efecto, se está moviendo la posición del punto original a lo largo de una trayectoria en línea recta hacia su nueva localización. De modo similar, una traslación es aplicable a un objeto que se define con múltiples posiciones de coordenadas, tales como cuadriláteros, mediante la recolocación de todas las posiciones de sus coordenadas, usando el mismo desplazamiento a lo largo de trayectorias paralelas
EN ESTE VÍDEO ANTERIOR SE NOS MOSTRÓ MAS DETALLADAMENTE LA FORMA DE LA TRASLACIÓN Y COMO NOSOTROS DE UNA MANERA FÁCIL PODEMOS REALIZARA
EN ESTE VIDEO SE NOS VIENE MOSTRANDO AL PRINCIPIO UN POQUIIIIITO DE LA HISTORIA DE LA TRASLACION PERO MAS ADELNTE NOS DA LA EINICION DE ELLA Y COMO POEMOS FORMARLA
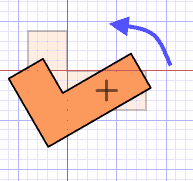
Se escoge un punto O llamado centro de rotación. Con el compás, se toma la medida desde el centro, hacia el vértice A y con ese radio se traza un arco de circunferencia.Marcamos el vértice rotado A’.Para rotar los otros vértices debemos medir el ángulo que corresponde al arco dibujado con el vértice A y mantenerlo, para que la forma de la figura no cambie. Además debemos conservar el ángulo de giro. La figura obtenida es congruente con la primera.
Y Resumiendo:
es 
.
es 
.
, y su representación cruza el eje de las abscisas dos veces.
, y su representación es tangente al eje de abscisas.
