Triángulo
Clasificación de los triángulos
[editar]
Según sus lados
|
|
[editar]
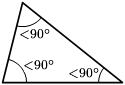
Según sus ángulos
|
|
Construcción de triángulos
Un triángulo, tiene tres lados y tres ángulos. Para construir un triángulo hay que conocer tres de esos datos, siendo al menos uno de ellos un lado:
- Conocidos los tres lados.
- Conocidos dos lados y el ángulo comprendido entre ellos.
- Conocido un lado y sus dos ángulos contiguos.
esta es una imágenes de algunos triángulos
acontinuacion podrán observar la construcción de triángulos
cuadriláteros
Un cuadrilátero es un polígono que tiene cuatro lados. Los cuadriláteros pueden tener distintas formas, pero todos ellos tienen cuatro vértices y dos diagonales, y la suma de sus ángulos internos siempre da como resultado 360º.
componentes de un cuadrilátero
Los componentes de un cuadrilátero son los siguientes:
- 4 vértices: puntos de intersección de los lados que conforman el cuadrilátero.
- 4 lados: segmentos limitados por dos vértices contiguos.
- 2 diagonales: segmentos cuyos extremos son dos vértices no contiguos.
- 4 ángulos interiores: conformados por dos lados y un vértice común.
- 4 ángulos exteriores: prolongación de los lados.
Los cuadriláteros se clasifican según el paralelismo de sus lados:
1. Paralelogramos: sus lados opuestos son paralelos
2. Trapecios: dos de sus lados son paralelos; los otros dos, no
3. Trapezoide: los lados no son paralelos
Taxonomía de los cuadriláteros
En el gráfico ilustrativo de la taxonomía de los cuadriláteros se pasa de las definiciones más generales a las más específicas siguiendo el sentido de las flechas.Así se parte de un cuadrilátero definido como un polígono cerrado de cuatro lados, sin más restricciones, para diferenciar los cuadriláteros compuestos de los simples.
En un cuadrilátero complejo, dos de sus lados se cortan. En uno simple los lados no se cruzan.
Los cuadriláteros simples se dividen en:
- Cóncavos. En un cuadrilátero cóncavo al menos uno de sus ángulos interiores mide más de 180º.
- Convexos. Un cuadrilátero convexo no tiene ángulos interiores que midan más de 180º. Los convexos se subdividen en:
- Cuadrilátero cíclico, si se puede trazar una circunferencia que pase por sus vértices.
- Cuadrilátero tangencial, si se puede trazar una circunferencia tangente a cada uno de sus lados.
- Trapecios, si tienen dos lados paralelos. Se diferencian:
- Romboide, como caso más general de paralelogramo, si los lados son paralelos dos a dos.
- Trapecio rectángulo, que tiene un lado perpendicular a sus bases.
- Trapecio isósceles, cuyos lados no paralelos son de igual medida. Este trapecio también es cíclico.
Un caso particular de trapecio isósceles es cuando la longitud de una de las bases es igual que la de sus lados, por lo cual se configura un trapecio de tres lados iguales.
El rectángulo es un cuadrilátero que simultáneamente cumple las características de:
- Paralelogramo, al ser paralelos sus lados opuestos.
- Trapecio rectángulo, porque los lados son perpendiculares a las bases.
- Trapecio isósceles, por ser de igual longitud los lados que no constituyen las bases.
Por último, el cuadrado puede considerarse rombo, rectángulo, con lados iguales y bicéntrico
estas son algunas imágenes de los cuadriláteros
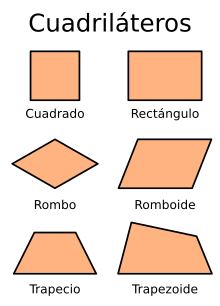
acontinuacion podemos observar como construir estos cuadriláteros
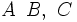 .
.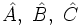 , aunque también son usuales las letras griegas:
, aunque también son usuales las letras griegas: 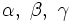 .
.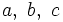 ; es la letra correspondiente al vértice opuesto al lado. También se puede expresar cada lado con dos letras mayúsculas:
; es la letra correspondiente al vértice opuesto al lado. También se puede expresar cada lado con dos letras mayúsculas: 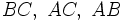 , las de los vértices contenidos en ese lado.
, las de los vértices contenidos en ese lado.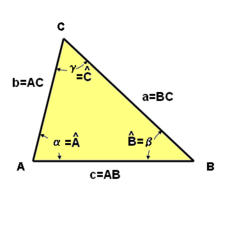



No hay comentarios:
Publicar un comentario